CLRS Solutions | Exercise 2.1-4

Consider the problem of adding two $n$-bit binary integers, stored in two $n$ element arrays $A$ and $B$. The sum of the two integers should be stored in binary form in an $(n + 1)$ element array $C$. State the problem formally and write pseudocode for adding the two integers.

The problem can be formally stated as…

Input: Two $n$ bit binary integers stored in two $n$ element array of binary digits (either 0 or 1) $A = \langle a_1, a_2, ... , a_n \rangle$ and $B = \langle b_1, b_2, ... , b_n \rangle$.

Output: A $(n + 1)$ bit binary integer stored in $(n + 1)$ element array of binary digits (either 0 or 1) $C = \langle c_1, c_2, ... , c_{n+1} \rangle$ such that $C = A + B$.

We also assume the binary digits are stored with least significant bit first, i.e. from right to left, first bit in index $1$, second bit in index $2$, and so on. Why we are doing this is discussed after the pseudocode.

$$\textsc {Add-Binary }(A, B)$$$$\begin{aligned}1& \quad n=\textsc {Max}(A.length,\,B.length) \\2& \quad \text {let }C[n+1]\text { be }\text { new }\text { array } \\3& \quad carry=0 \\4& \quad \textbf {for }i=1\textbf { to }n \\5& \quad \qquad C[i]=\textsc {}(A[i]+B[i]+carry)\mod2 \\6& \quad \qquad carry=\lfloor \textsc {}(A[i]+B[i]+carry)/2\rfloor \\7& \quad C[n+1]=carry \\8& \quad \textbf {return }C \\\end{aligned}$$

Left to Right or Right to Left

An earlier version of the solution presented here assumed the least significant bit was stored in index $n$ instead of index $1$. Which made the solution not only wrong (it did not handle all possible cases properly), it also caused a great deal of confusion in the comments section.

Here is why assuming least significant bit in index $n$ will make the problem unnecessarily complicated.

Consider the following two binary additions

Binary Addition

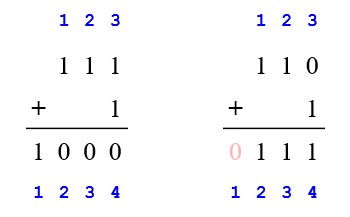
The one on the left adds $111_b$ and $1_b$ to $1000_b$. In this case, $n = 3$ and we end up with final array $C$ of length $n + 1 = 4$. The array indices are shown in blue with the assumption of storing bits as we they appear visually from left to right, i.e. most significant bit in first index and least significant bit in last index, $n$.

In this particular case there is no complication, and we could have just designed our pseudocode to iterate from the opposite direction, from $n$ downto $1$, and stored the result of the addition in line 4 in $C[i + 1]$ and the final $carry$ in line 6 in $C[1]$.

However, note that for the addition on the right, $110_b$ and $1_b$ sums up to $111_b$, and we end up with final array $C$ of length $n = 3$. In this case, $C[1]$ is empty (highlighted with light red), and we are left with the additional task of shifting all the elements to the left to meet our initial assumption of having most significant bit at index $1$.

One can argue that having zero in the first index is not a deal breaker, but depending on the use case it might add up to redundant work. For example, let’s say we need to repeatedly do this addition. And every time we end up with a case like the right one. Then we would keep on adding redundant zeroes in the beginning of the resulting array.

Python Code

# Bitwise binary addition of two lists # containing binary digits with least significant bit first def AddBinary(A, B): carry = 0 n = max(len(A), len(B)) C = [0 for i in range(n + 1)] for i in range(n): # One of A and B has length less than n # We need to treat index out of bound for that array # This is not explicitly handled in pseudocode a = A[i] if i < len(A) else 0 b = B[i] if i < len(B) else 0 # Modulo for sum and integer division for carry C[i] = (a + b + carry) % 2 carry = (a + b + carry) // 2 C[n] = carry return C # Utility function for converting decimal to binary def DecimalToBinary(num): if num == 0: return [0] ret = [] while num > 0: ret.append(num & 1) num = num >> 1 return ret # Utility function for converting binary to decimal def BinaryToDecimal(lst): num = 0 for i in range(len(lst)): num += lst[i] << i return num # Test import random num_failed = 0 total_tests = 100 for i in range(total_tests): # Create two random integers a = random.randint(0, 10000) b = random.randint(0, 10000) a_ = DecimalToBinary(a) b_ = DecimalToBinary(b) sum = BinaryToDecimal(AddBinary(a_, b_)) # Check if the sum is correct if sum != (a + b): num_failed += 1 print(f"#{i:<2} {a} + {b} = {sum} [Expected {(a + b)}]") if num_failed > 0: print(f"\nFailed {num_failed}/{total_tests}") else: print(f"Passed {total_tests}/{total_tests} tests")