We can build a heap by repeatedly calling \(\textsc{Max-Heap-Insert}\) to insert the elements into the heap. Consider the following variation on the \(\textsc{Build-Max-Heap}\) procedure:
$$\textsc{Build-Max-Heap}'(A)$$$$\begin{aligned} 1& \quad A.heap\text{-}size\,=\,1 \\ 2& \quad \textbf{for }\,i\,=\,2\textbf{ to }\,A.length \\ 3& \quad \qquad \textsc{Max-Heap-Insert}(A, \, A[i]) \\ \end{aligned}$$
- Do the procedures \(\textsc{Build-Max-Heap}\) and \(\textsc{Build-Max-Heap}'\) always create the same heap when run on the same input array? Prove that they do, or provide a counterexample.
- Show that in the worst case, \(\textsc{Build-Max-Heap}'\) requires \(\Theta (n \lg n)\) time to build an \(n\)-element heap.
A
Think of how a heap grows when you build it. The standard \(\textsc{Build-Max-Heap}\) works from the bottom up, starting with the second-to-last level and calling \(\textsc{Max-Heapify}\) on each node as it moves upward. In contrast, \(\textsc{Build-Max-Heap}'\) builds the heap incrementally by inserting elements one at a time from left to right.
These two approaches take fundamentally different paths through the space of possible heap configurations. While both end up with valid max-heaps, they don’t necessarily produce the same heap structure.
Consider a simple counterexample with the array \(A = \langle 1, 2, 3 \rangle\).
Using \(\textsc{Build-Max-Heap}\):
Starting with the array representation \(\langle 1, 2, 3 \rangle\), we begin at \(i = \lfloor 3/2 \rfloor = 1\). When we call \(\textsc{Max-Heapify}(A, 1)\), element 1 compares with its children 2 and 3. The largest child is 3, so we swap 1 and 3, giving us \(\langle 3, 2, 1 \rangle\).
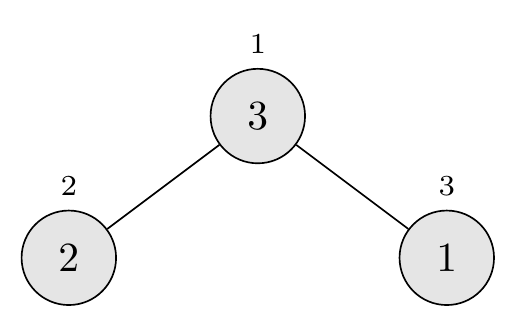
Using \(\textsc{Build-Max-Heap}'\):
We start with heap-size = 1, so the heap initially contains just element 1. When we insert 2, it becomes the left child of 1, but since 2 > 1, it bubbles up to become the root, giving us \(\langle 2, 1 \rangle\). When we insert 3, it becomes the right child of 2, but since 3 > 2, it bubbles up to become the root, giving us \(\langle 3, 1, 2 \rangle\).
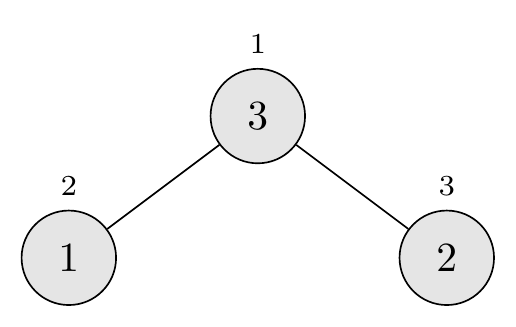
The final heaps are \(\langle 3, 2, 1 \rangle\) and \(\langle 3, 1, 2 \rangle\), which are different. So, no, \(\textsc{Build-Max-Heap}\) and \(\textsc{Build-Max-Heap}'\) do not always create the same heap.
But both heaps are valid max-heaps (they both satisfy the max-heap property), even though they have different structures. This shows that there can be multiple valid max-heap representations for the same set of elements.
B
To understand the worst-case running time, think about what happens when we repeatedly insert elements into a growing heap. Each insertion takes time proportional to the height of the heap at that moment.
When we insert the \(i\)-th element, the heap contains \(i-1\) elements, so its height is \(\lfloor \lg(i-1) \rfloor\). The cost of inserting this element is \(O(\lg i)\).
The total cost is the sum of all insertion costs:
\[\begin{align*} T(n) &= \sum_{i=2}^{n} O(\lg i) \\ &= O\left(\sum_{i=2}^{n} \lg i\right) \\ &= O(\lg(n!)) \end{align*}\]Using Stirling’s approximation, we know that \(\lg(n!) = \Theta(n \lg n)\). We can also see this more directly by noting that:
\[\begin{align*} \sum_{i=2}^{n} \lg i &\geq \sum_{i=n/2}^{n} \lg i \\ &\geq \sum_{i=n/2}^{n} \lg(n/2) \\ &= (n/2) \cdot \lg(n/2) \\ &= \Theta(n \lg n) \end{align*}\]This lower bound shows that in the worst case (which actually occurs for many input orderings), \(\textsc{Build-Max-Heap}'\) requires \(\Theta(n \lg n)\) time.
This is in contrast to the standard \(\textsc{Build-Max-Heap}\), which runs in \(O(n)\) time. The key difference is that \(\textsc{Build-Max-Heap}\) exploits the fact that most nodes in a heap are near the bottom, where \(\textsc{Max-Heapify}\) is cheap. In contrast, \(\textsc{Build-Max-Heap}'\) inserts elements when the heap is already partially filled, requiring logarithmic-time insertions for most elements.