Illustrate the operation of \(\textsc{Max-Heap-Insert}(A, 10)\) on the heap \(A = \langle 15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1 \rangle\).
The \(\textsc{Max-Heap-Insert}\) operation adds a new element to the max-heap while maintaining the heap property. Think of it like adding a new high-priority task to a job scheduler. The new element starts at the bottom and “bubbles up” until it finds its proper position.
Initial heap
\(A = \langle 15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1 \rangle\) with \(\text{heap-size} = 12\)
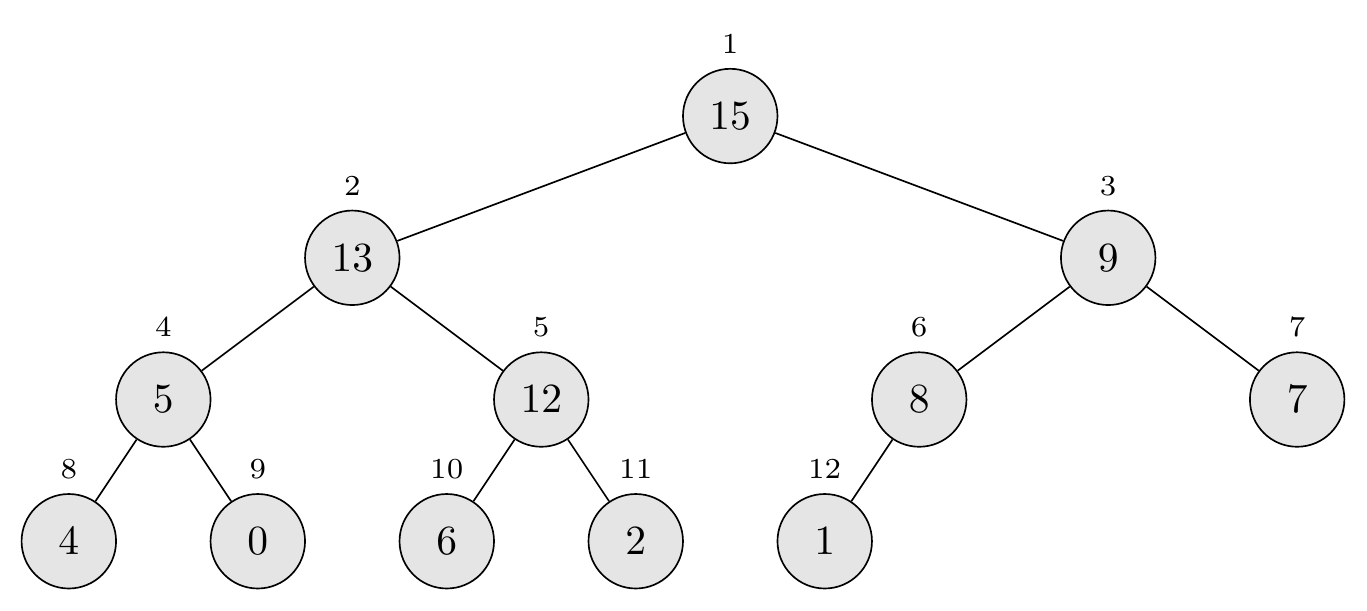
Step #1
Expand the heap by incrementing heap-size.
\[\text{heap-size} = 13\]Step #2
Add a new leaf with key \(-\infty\) (a sentinel value smaller than any actual key).
\[A[13] = -\infty\]The array becomes: \(\langle 15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1, -\infty \rangle\)
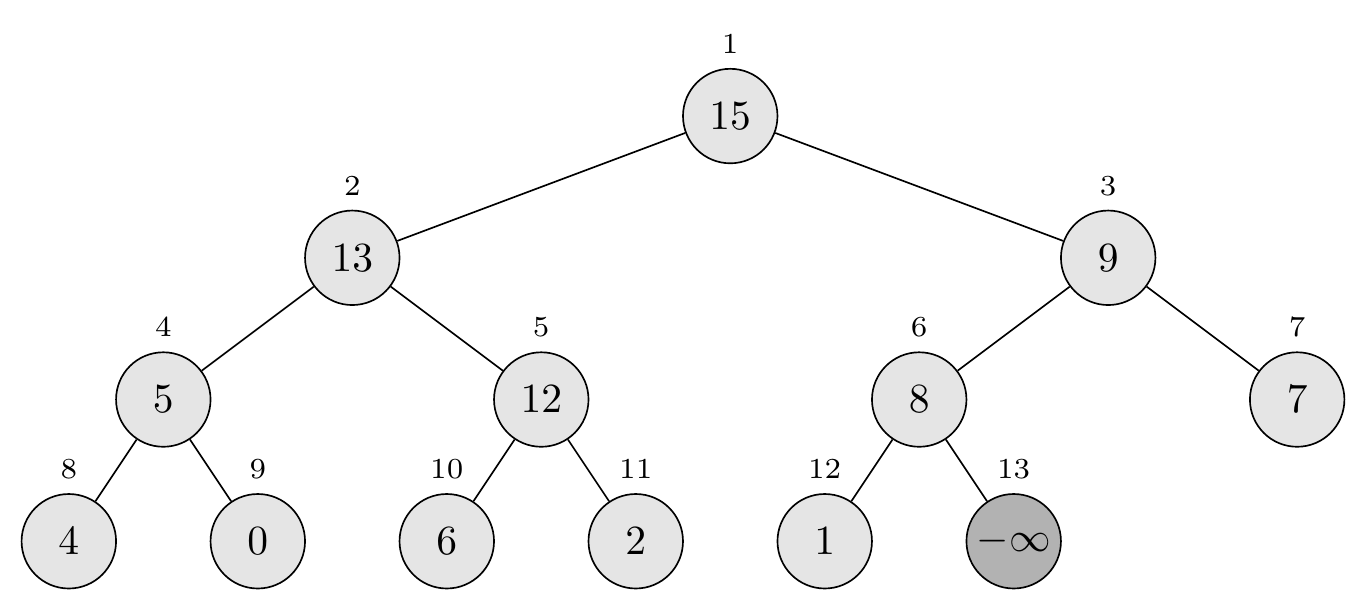
Step #3
Call \(\textsc{Heap-Increase-Key}(A, 13, 10)\) to set the key to 10.
The procedure sets \(A[13] = 10\) and then bubbles it up.
\[A[13] = 10\]Compare with parent: \(A[6] = 8 < A[13] = 10\), so swap:
\[\langle 15, 13, 9, 5, 12, 10, 7, 4, 0, 6, 2, 1, 8 \rangle\]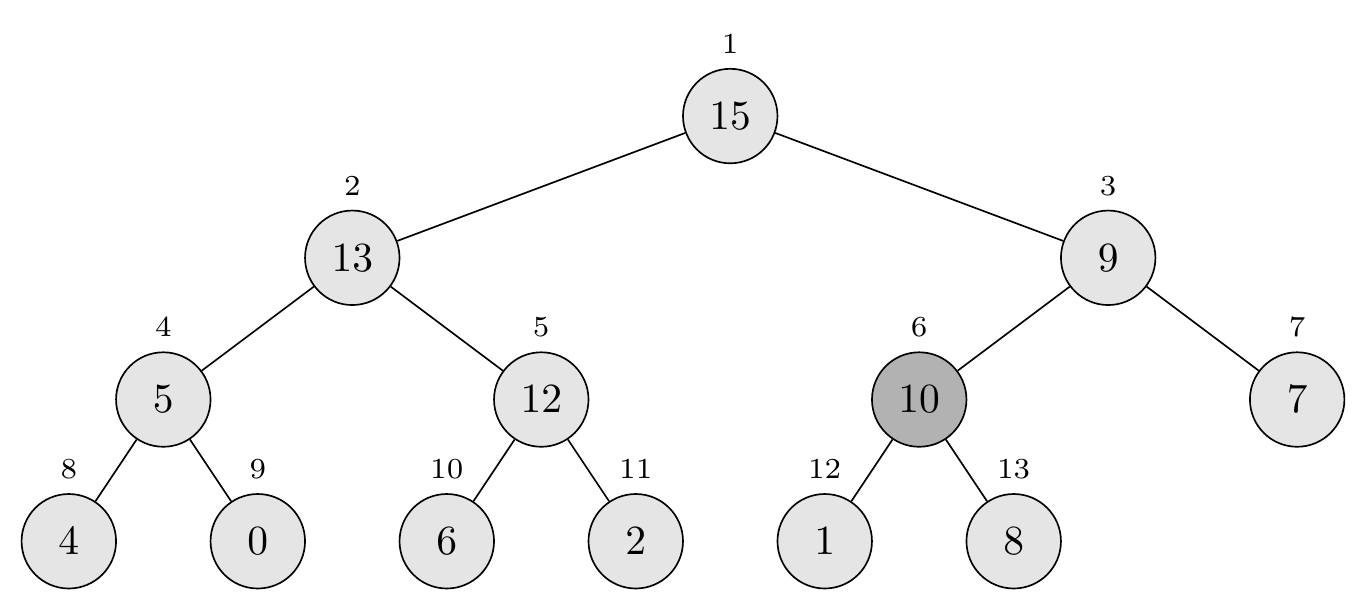
Compare with parent: \(A[3] = 9 < A[6] = 10\), so swap:
\[\langle 15, 13, 10, 5, 12, 9, 7, 4, 0, 6, 2, 1, 8 \rangle\]Compare with parent: \(A[1] = 15 > A[3] = 10\), so the heap property is satisfied. Stop.
Final result
\[A = \langle 15, 13, 10, 5, 12, 9, 7, 4, 0, 6, 2, 1, 8 \rangle\]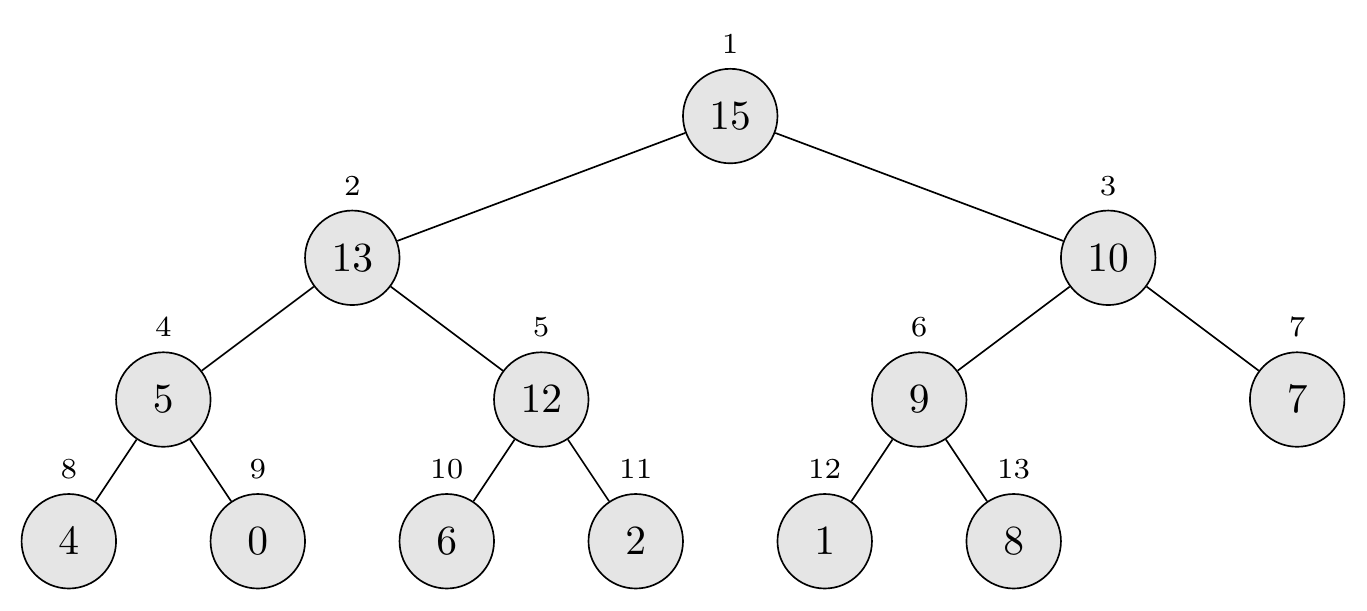
The new element (10) has found its correct position in the heap, maintaining the max-heap property that every parent is greater than or equal to its children. The operation runs in \(O(\lg n)\) time because the element can bubble up at most the height of the tree.