Illustrate the operation of \(\textsc{Heap-Extract-Max}\) on the heap \(A = \langle 15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1 \rangle\).
The \(\textsc{Heap-Extract-Max}\) operation removes and returns the maximum element (the root) from the max-heap. Think of it like removing the highest-priority job from a task scheduler. The operation must maintain the max-heap property after removal.
Here’s how \(\textsc{Heap-Extract-Max}\) works step by step on the given heap:
Initial heap
\[A = \langle 15, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2, 1 \rangle\]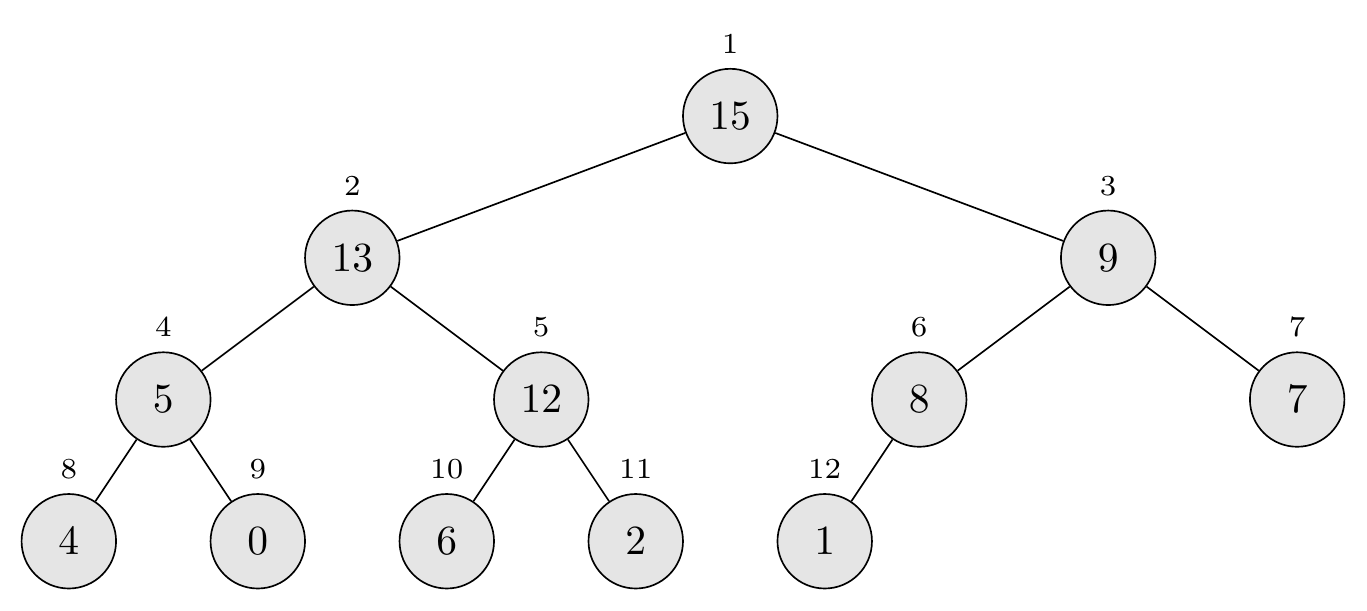
Step #1
Save the maximum value (the root).
\[\text{max} = A[1] = 15\]Step #2
Move the last element to the root and reduce the heap size by 1.
\[A[1] = A[12] = 1\]The array becomes: \(\langle 1, 13, 9, 5, 12, 8, 7, 4, 0, 6, 2 \rangle\) (with heap-size = 11)
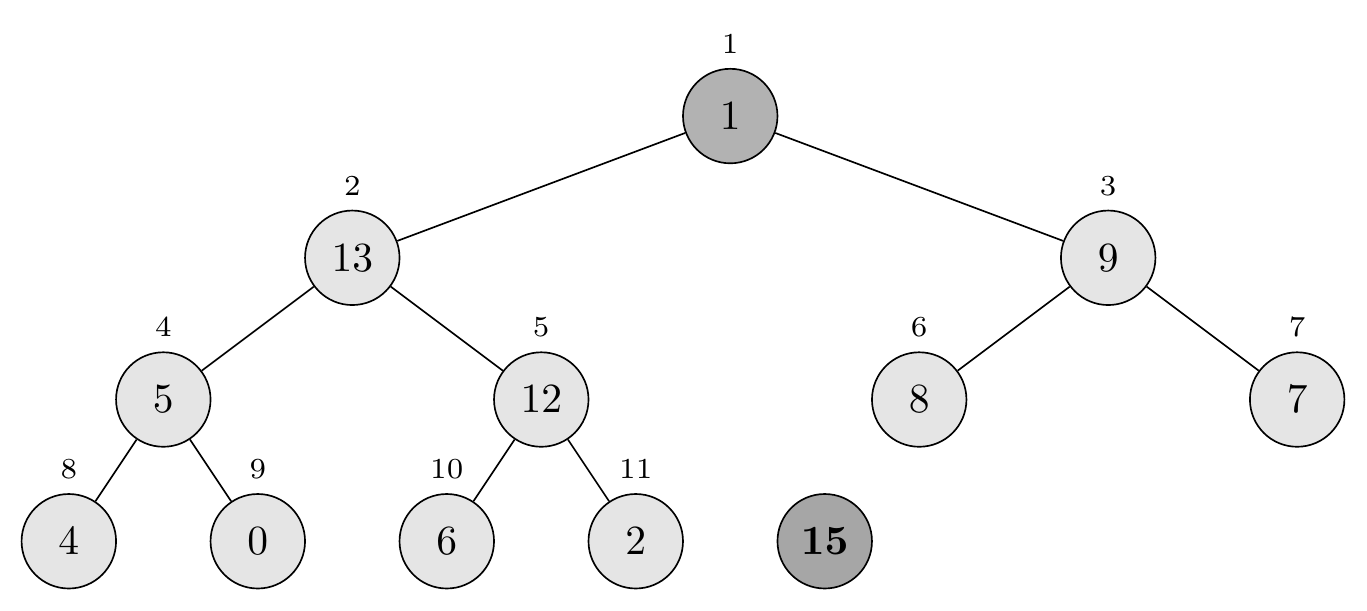
Step 3
Decrease heap-size and call \(\textsc{Max-Heapify}(A, 1)\).
The \(\textsc{Max-Heapify}\) procedure restores the heap property by letting the small value “float down.”
First comparison: \(A[1] = 1\) vs. children \(A[2] = 13\) and \(A[3] = 9\). Largest is 13, so swap \(A[1]\) with \(A[2]\):
\[\langle 13, 1, 9, 5, 12, 8, 7, 4, 0, 6, 2 \rangle\]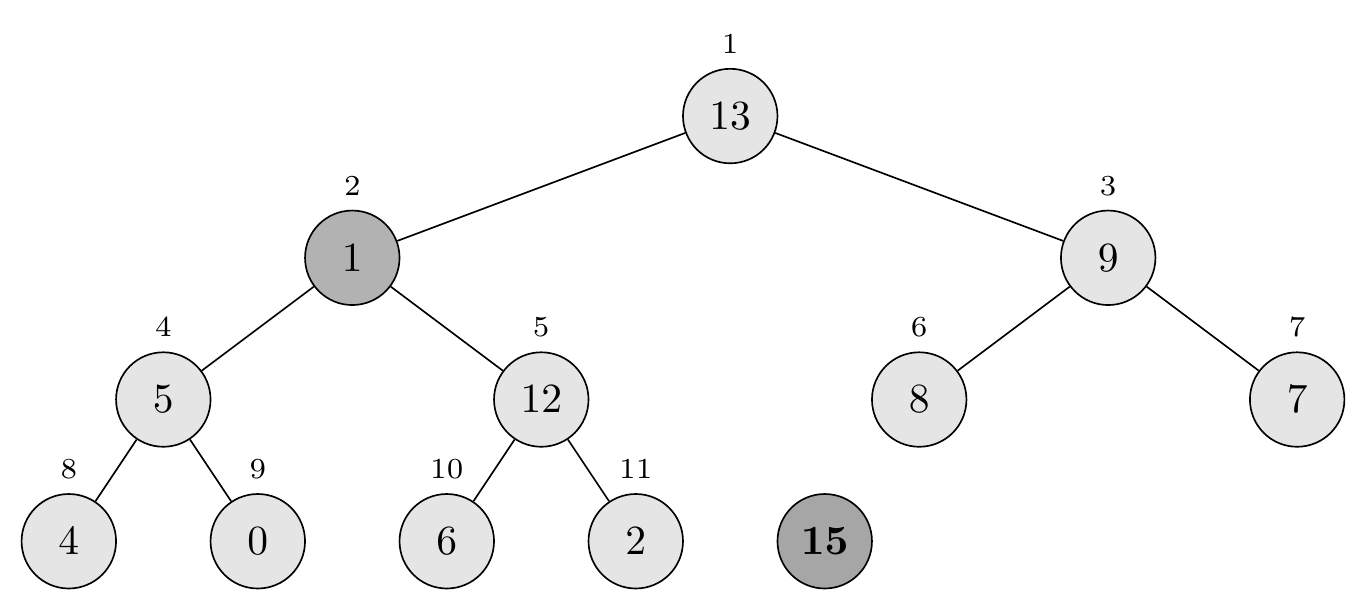
Second comparison: \(A[2] = 1\) vs. children \(A[4] = 5\) and \(A[5] = 12\). Largest is 12, so swap \(A[2]\) with \(A[5]\):
\[\langle 13, 12, 9, 5, 1, 8, 7, 4, 0, 6, 2 \rangle\]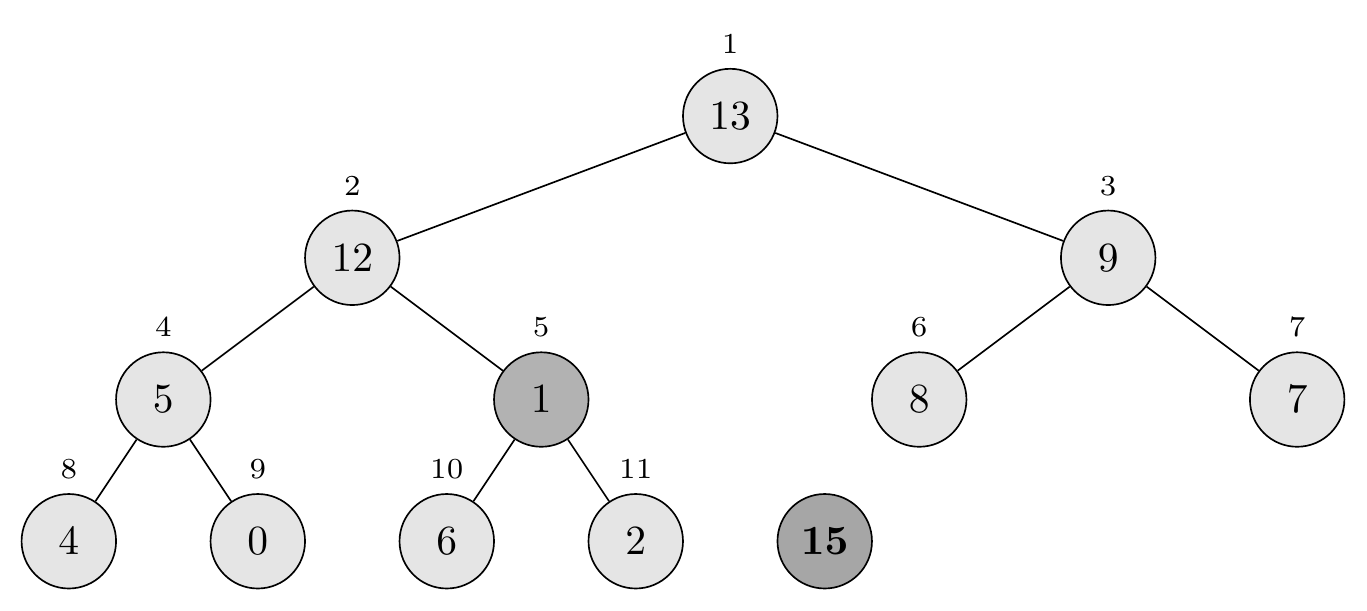
Third comparison: \(A[5] = 1\) vs. children \(A[10] = 6\) and \(A[11] = 2\). Largest is 6, so swap \(A[5]\) with \(A[10]\):
\[\langle 13, 12, 9, 5, 6, 8, 7, 4, 0, 1, 2 \rangle\]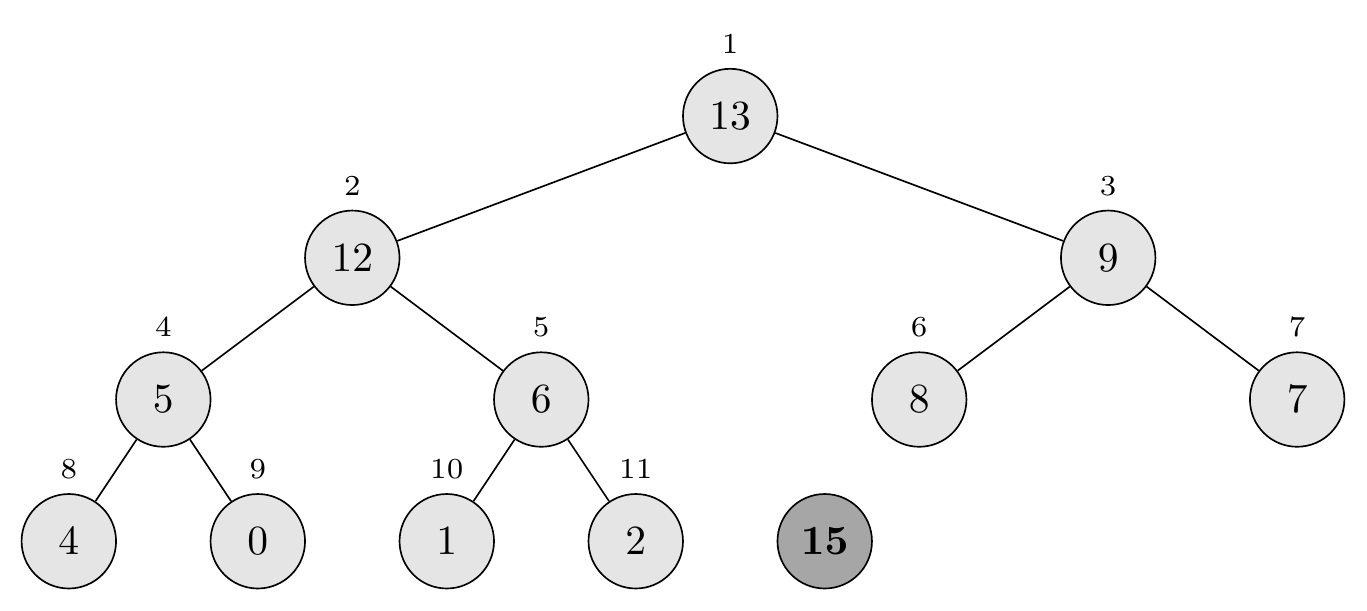
Node 10 is a leaf, so \(\textsc{Max-Heapify}\) terminates.
Final result
The procedure returns \(\text{max} = 15\), and the resulting heap is:
\[A = \langle 13, 12, 9, 5, 6, 8, 7, 4, 0, 1, 2 \rangle\]This demonstrates how \(\textsc{Heap-Extract-Max}\) efficiently removes the maximum element in \(O(\lg n)\) time by replacing the root with the last element and restoring the heap property through successive comparisons and swaps down the tree.