Using Figure 6.3 as a model, illustrate the operation of \(\textsc{Build-Max-Heap}\) on the array \(A = \langle 5, 3, 17, 10, 84, 19, 6, 22, 9 \rangle\).
The key insight behind \(\textsc{Build-Max-Heap}\) is that it works bottom-up, starting from the last non-leaf node and moving toward the root. Think of it like organizing a corporate hierarchy: you first make sure each department head is the strongest person in their team, then ensure division managers are stronger than their department heads, and finally ensure the CEO is the strongest person in the company. It will probably be a very toxic place, but that’s the best I can think of for now.
For our array with 9 elements, we start at index \(\lfloor 9/2 \rfloor = 4\) because all nodes after this are leaves (which are already valid single-element heaps). We then call \(\textsc{Max-Heapify}\) on each node from 4 down to 1.
Initial Configuration
The input array is:
\[A = \langle 5, 3, 17, 10, 84, 19, 6, 22, 9 \rangle\]Visualizing this as a binary tree:
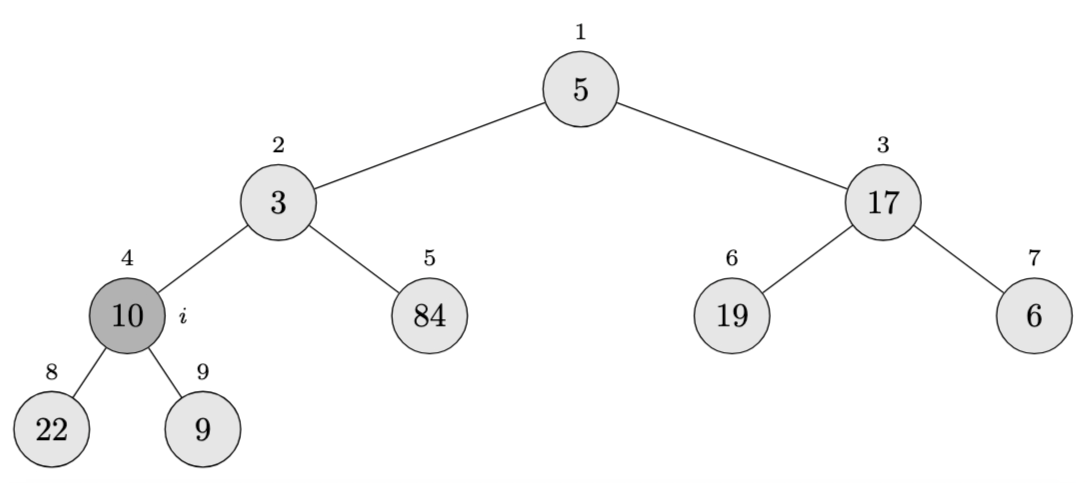
The algorithm starts at \(i = \lfloor 9/2 \rfloor = 4\).
Step 1
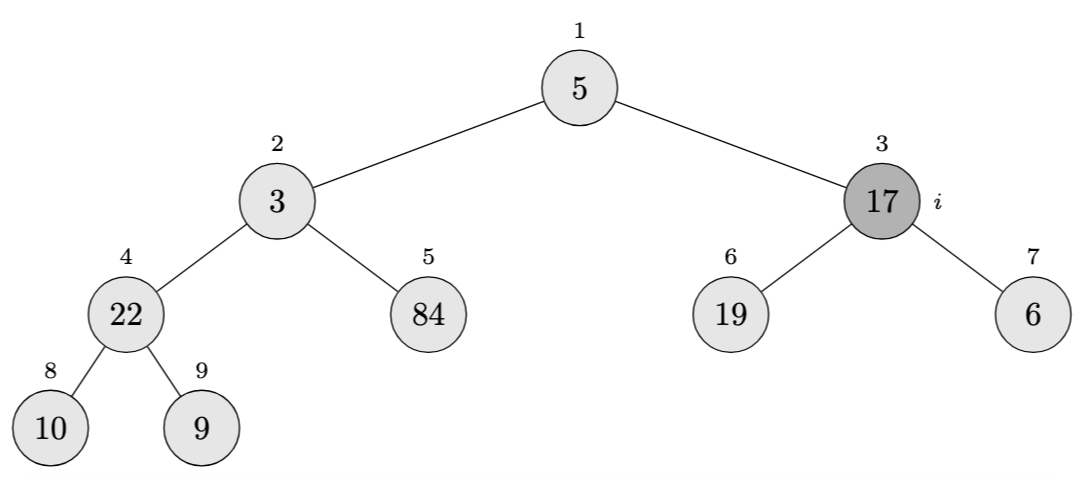
Call \(\textsc{Max-Heapify}(A, 4)\):
- Left child: index 8 (value 22)
- Right child: index 9 (value 9)
- Since 22 > 10, swap them
Array becomes: \(\langle 5, 3, 17, 22, 84, 19, 6, 10, 9 \rangle\)
Step 2
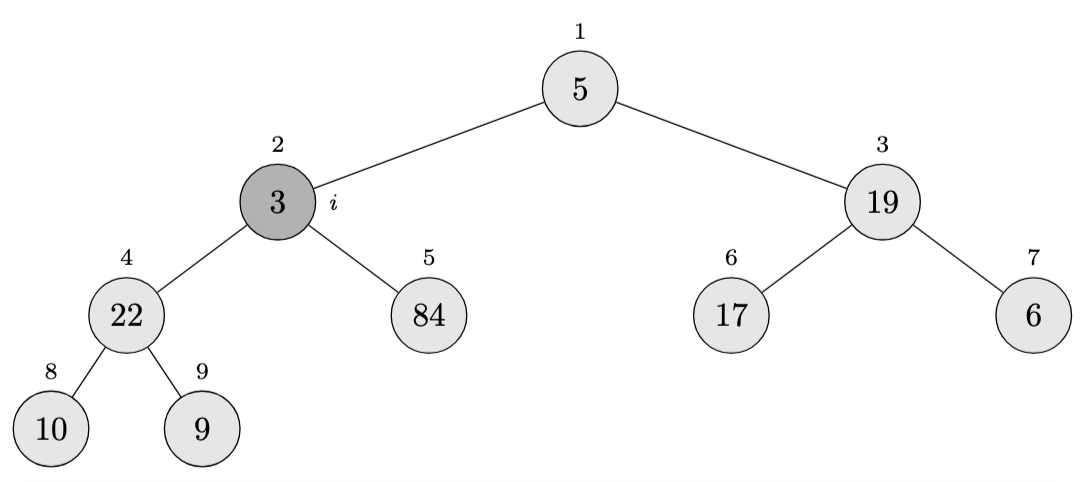
Call \(\textsc{Max-Heapify}(A, 3)\):
- Left child: index 6 (value 19)
- Right child: index 7 (value 6)
- Since 19 > 17, swap them
Array becomes: \(\langle 5, 3, 19, 22, 84, 17, 6, 10, 9 \rangle\)
Step 3
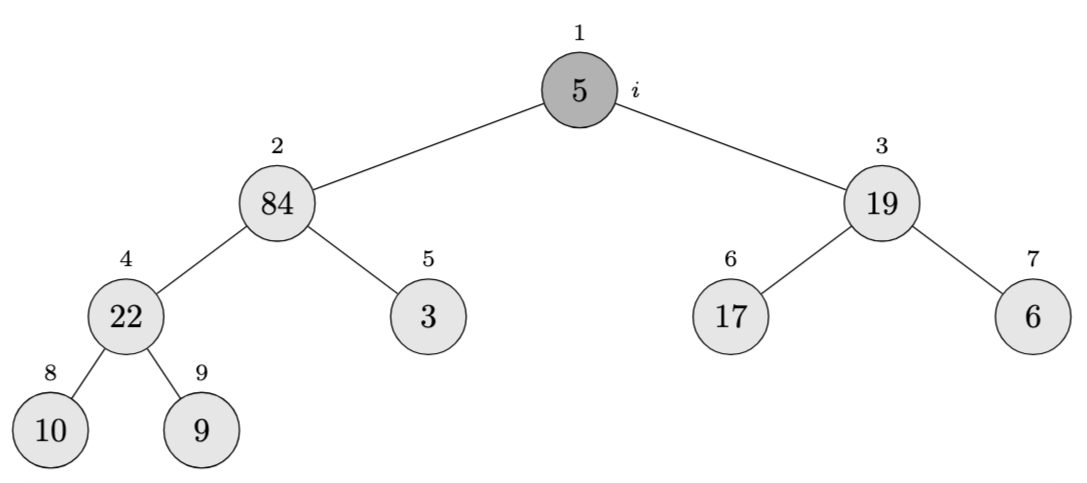
Call \(\textsc{Max-Heapify}(A, 2)\):
- Left child: index 4 (value 22)
- Right child: index 5 (value 84)
- Since 84 > 3, swap them
Array becomes: \(\langle 5, 84, 19, 22, 3, 17, 6, 10, 9 \rangle\)
Step 4
Call \(\textsc{Max-Heapify}(A, 1)\):
- Left child: index 2 (value 84)
- Right child: index 3 (value 19)
- Since 84 > 5, swap them
Array becomes: \(\langle 84, 5, 19, 22, 3, 17, 6, 10, 9 \rangle\)
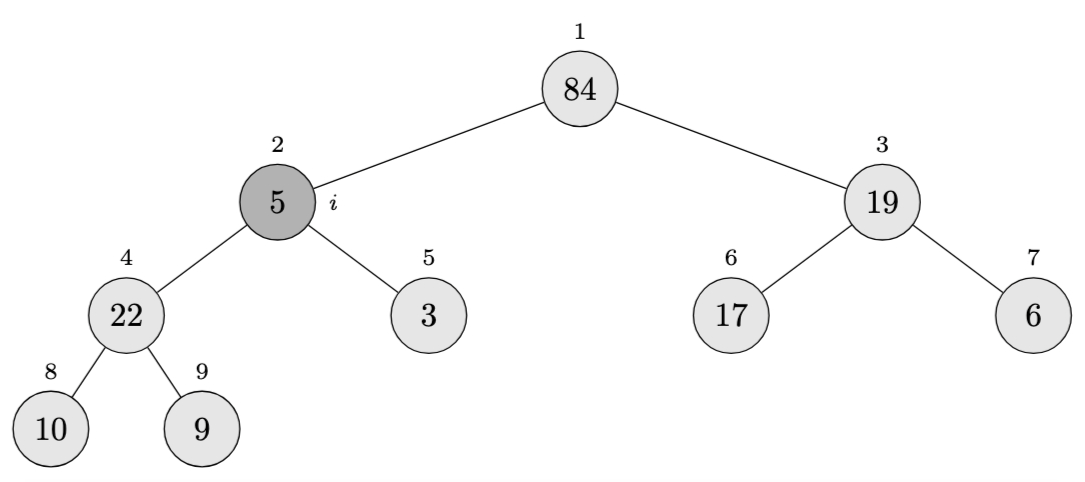
Coincidentally, all calls to \(\textsc{Max-Heapify}\) before this, had involved just one swap. But this time, we’ll have to recursively call \(\textsc{Max-Heapify}(A, 2)\) and so on:
- Left child: index 4 (value 22)
- Right child: index 5 (value 3)
- Since 22 > 5, swap them
Array becomes: \(\langle 84, 22, 19, 5, 3, 17, 6, 10, 9 \rangle\)
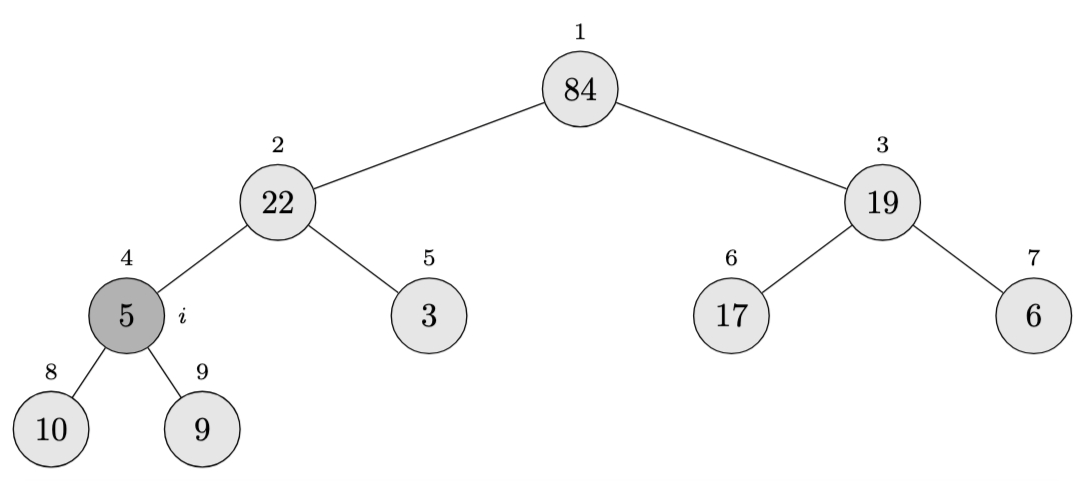
Another recursive call to \(\textsc{Max-Heapify}(A, 4)\):
- Left child: index 8 (value 10)
- Right child: index 9 (value 9)
- Since 10 > 5, swap them
Final Result
Array: \(\langle 84, 22, 19, 10, 3, 17, 6, 5, 9 \rangle\)
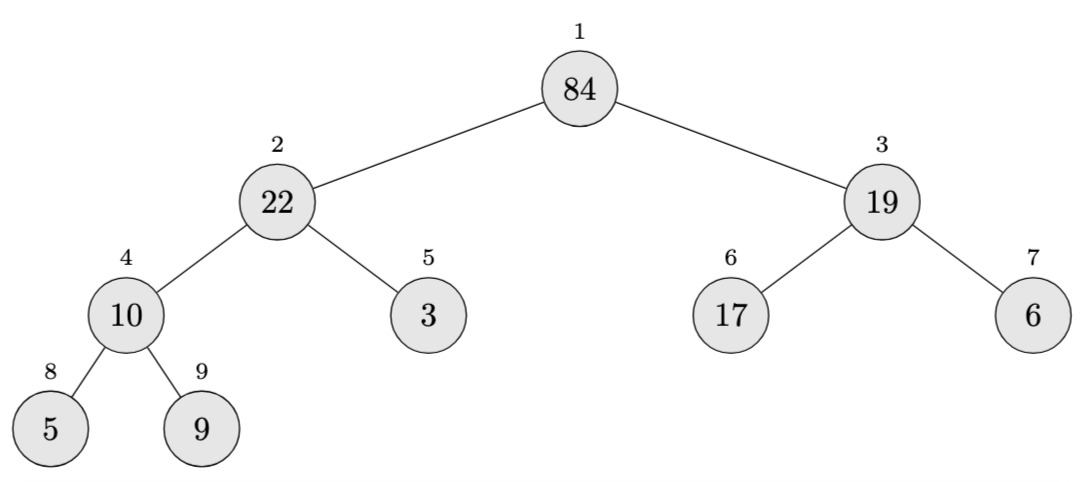
This is now a valid max-heap where every parent is greater than or equal to its children.