Show that the worst-case running time of \(\textsc{Max-Heapify}\) on a heap of size \(n\) is \(\Omega(\lg n)\). (Hint: For a heap with \(n\) nodes, give node values that cause \(\textsc{Max-Heapify}\) to be called recursively at every node on a simple path from the root down to a leaf.)
We already know that \(\textsc{Max-Heapify}\) runs in \(O(\lg n)\) time because it can make at most \(h\) recursive calls, where \(h = \lfloor \lg n \rfloor\) is the height of the heap. To show that the worst-case running time is \(\Omega(\lg n)\), we need to demonstrate that there exists an input configuration that forces the algorithm to take at least \(\Omega(\lg n)\) time.
The worst case occurs when the element at the root needs to sink all the way down to a leaf, causing \(\textsc{Max-Heapify}\) to recurse at every level of the tree. We can construct such a heap by placing the smallest element at the root and arranging the remaining elements so that at each step, the violating element is always smaller than at least one of its children.
Here’s a concrete example: Consider a heap where the root contains 1 (the smallest value), and all other nodes contain values greater than 1, arranged in increasing order from left to right at each level. For instance, with a complete binary tree:
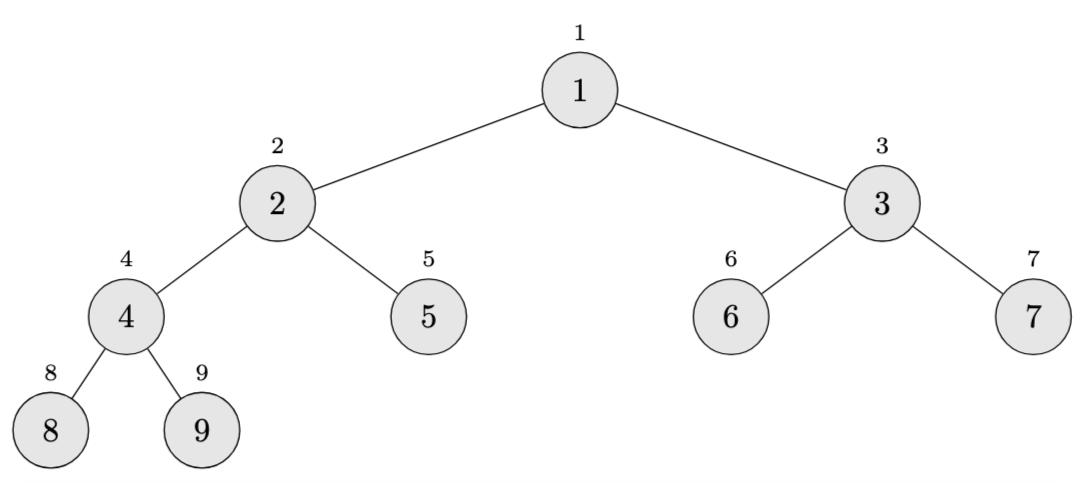
When we call \(\textsc{Max-Heapify}(A, 1)\) on this heap:
- At the root, we compare 1 with children 2 and 3. The largest is 3, so we exchange 1 with 3
- Now 1 is at position 3, with children 6 and 7. The largest is 7, so we exchange 1 with 7
- Now 1 is at position 7 (a leaf in this example), and the procedure terminates
More generally, to force the maximum number of recursive calls, we can construct a heap of size \(n\) where:
- The root contains the smallest value (say, 1)
- For every internal node along the rightmost path from root to leaf, ensure it has at least one child larger than it
- Arrange values so that at each step, we always choose the right child (or any child that leads to the longest path)
Since a heap of \(n\) elements has height \(\lfloor \lg n \rfloor\), and our construction forces \(\textsc{Max-Heapify}\) to traverse a path from root to leaf, the algorithm performs \(\Theta(\lg n)\) work: one comparison and one exchange at each of the \(\Theta(\lg n)\) levels.
Therefore, the worst-case running time is \(\Omega(\lg n)\).
Combined with the upper bound \(O(\lg n)\) established in the text, we conclude that the worst-case running time of \(\textsc{Max-Heapify}\) is \(\Theta(\lg n)\).