Using Figure 6.2 as a model, illustrate the operation of \(\textsc{Max-Heapify}(A, 3)\) on the array \(A = \langle 27, 17, 3, 16, 13, 10, 1, 5, 7, 12, 4, 8, 9, 0 \rangle\).
To understand what happens when we call \(\textsc{Max-Heapify}(A, 3)\), we need to trace through how the value at position 3 (which is 3) moves down the heap. The procedure assumes that the subtrees rooted at the left and right children are already max-heaps, but the element at position 3 might violate the max-heap property by being smaller than its children.
Let’s visualize the initial heap structure. The array has 14 elements, so position 3 has:
- Left child at position \(2 \times 3 = 6\) with value 10
- Right child at position \(2 \times 3 + 1 = 7\) with value 1
Since 3 is smaller than its left child (10), it violates the max-heap property and needs to be exchanged.
Initial configuration (before the call):
Array: \(\langle 27, 17, 3, 16, 13, 10, 1, 5, 7, 12, 4, 8, 9, 0 \rangle\)
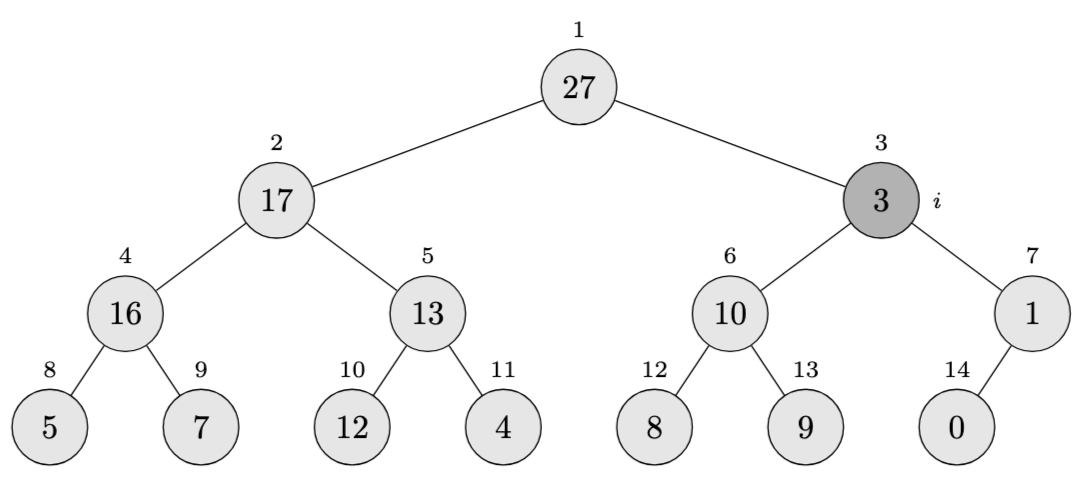
Step 1: Call \(\textsc{Max-Heapify}(A, 3)\)
Compare \(A[3] = 3\) with its children:
- Left child: \(A[6] = 10\)
- Right child: \(A[7] = 1\)
The largest is \(A[6] = 10\), so we exchange \(A[3]\) with \(A[6]\).
Array after exchange: \(\langle 27, 17, 10, 16, 13, 3, 1, 5, 7, 12, 4, 8, 9, 0 \rangle\)
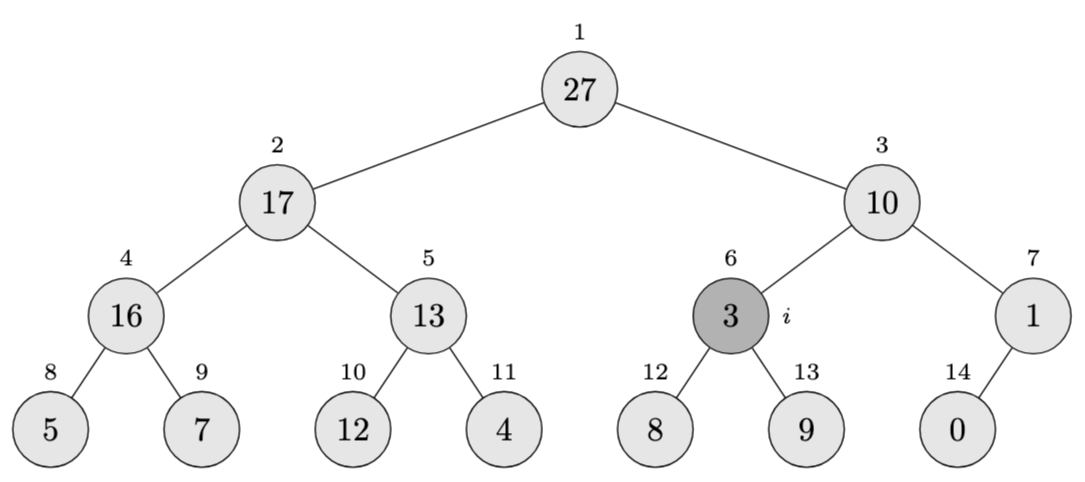
Step 2: Recursively call \(\textsc{Max-Heapify}(A, 6)\)
Now we need to check position 6 (which now contains 3):
- Left child: \(A[12] = 8\)
- Right child: \(A[13] = 9\)
The largest is \(A[13] = 9\), so we exchange \(A[6]\) with \(A[13]\).
Array after exchange: \(\langle 27, 17, 10, 16, 13, 9, 1, 5, 7, 12, 4, 8, 3, 0 \rangle\)
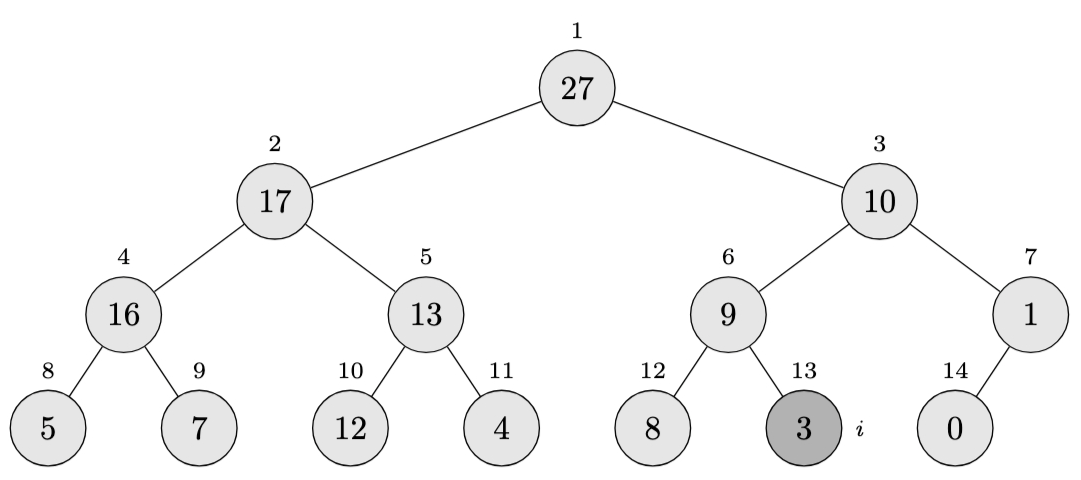
Step 3: Position 13 is a leaf
Since position 13 has no children (\(2 \times 13 = 26 > 14\)), it’s a leaf node and the procedure terminates.
Final array: \(\langle 27, 17, 10, 16, 13, 9, 1, 5, 7, 12, 4, 8, 3, 0 \rangle\)
The element 3 has “floated down” from position 3 to position 13, and the max-heap property is now satisfied throughout the subtree that was originally rooted at position 3.