Is the array with values \(\langle 23, 17, 14, 6, 13, 10, 1, 5, 7, 12 \rangle\) a max-heap?
To determine if this array is a max-heap, we need to check whether the max-heap property holds for every node. Recall that the max-heap property states that for every node \(i\) other than the root:
\[A[\textsc{Parent}(i)] \ge A[i]\]Equivalently, we can check that each parent is greater than or equal to both of its children (if they exist). Let’s systematically verify this for each internal node.
The array as a binary tree looks like:
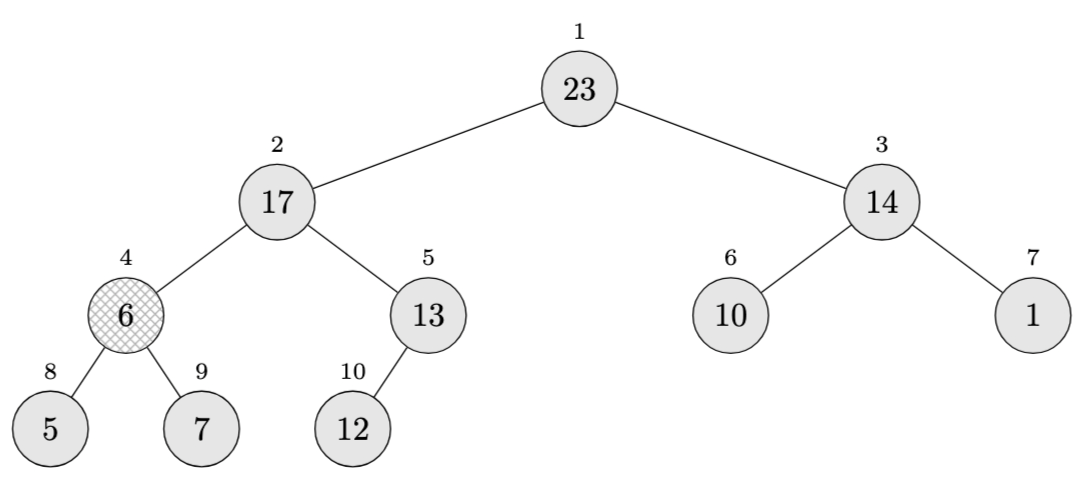
Now let’s check each internal node:
- Node 1 (value 23): Children are 17 and 14. Since \(23 \ge 17\) and \(23 \ge 14\), this is fine.
- Node 2 (value 17): Children are 6 and 13. Since \(17 \ge 6\) and \(17 \ge 13\), this is fine.
- Node 3 (value 14): Children are 10 and 1. Since \(14 \ge 10\) and \(14 \ge 1\), this is fine.
- Node 4 (value 6): Children are 5 and 7. We have \(6 \ge 5\), but \(6 \not\ge 7\). Violation!
- Node 5 (value 13): Left child is 12. Since \(13 \ge 12\), this is fine.
So, no, this array is not a max-heap. The max-heap property is violated at node 4, where the parent value (6) is less than its right child (7).