Is an array that is in sorted order a min-heap?
Yes, a sorted array (in increasing order) is always a min-heap. Let’s see why this is true.
For an array to be a min-heap, it must satisfy the min-heap property: for every node \(i\) other than the root, we must have:
\[A[\textsc{Parent}(i)] \le A[i]\]In other words, every parent must be less than or equal to its children. Now consider a sorted array \(A[1], A[2], \ldots, A[n]\) where \(A[1] \le A[2] \le \cdots \le A[n]\).
For any node at index \(i\), its parent is at index \(\lfloor i/2 \rfloor\) and its children (if they exist) are at indices \(2i\) and \(2i + 1\). We need to verify that:
\[A[\lfloor i/2 \rfloor] \le A[i]\]Since the array is sorted and \(\lfloor i/2 \rfloor < i\) (for all \(i > 1\)), we have:
\[A[\lfloor i/2 \rfloor] \le A[i]\]This holds for all nodes \(i > 1\), so the min-heap property is satisfied everywhere.
For example, the sorted array \(\langle 1, 2, 3, 4, 5, 6, 7 \rangle\) is a valid min-heap. As a tree, it looks like:
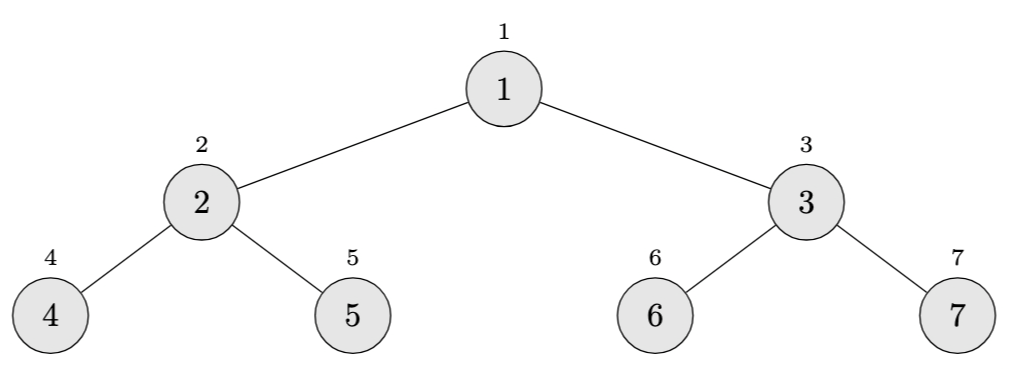
Each parent is indeed smaller than its children.